here we go again, another papervision3D demo featuring math permeated lines. this time im working with a classic piece of code known as the PQ torus. the vague idea is that you have 2 numbers (P + Q) that are used in the algorithm to define the knot. in general, given P + Q mutually prime, the line wraps meridionally around the torus P times and wraps the longitudinally around it Q times. i was having some trouble grasping exactly how this was going to be achieved, until i read this article on blackpawn’s website. he really breaks down the algo to a very simplistic level...

calculus

r = .5 * (2 + sin(Q * Φ))
x = r * cos(P * Φ)
y = r * cos(Q * Φ)
z = r * sin(P * Φ)

simple right? lol.
so Φ (or phi in my code) is basically a variable that is definded by change. in this case, im simply incrementing phi + .02 every frame. this seeds the math and gives you the cool visual effect.

anyway, after getting a handle on the math, writing the demo code was a snap. i took the existing code i wrote from the 3D object tracer and the lorenz attractor and combined them. (i also found + fixed an error for computing the line gradient color) i started out by allowing the users to only select values for PQ and that actually made sense.

but after some experimentation i found that using some unorthodox values for P+Q could net some very interesting results. take a look at some of these...

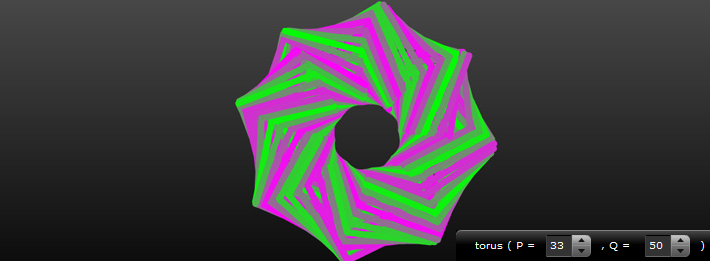
click here to check out the demo
and click here to view the source